3 - La Bremsstrahlung istantanea
Il primo esempio, che serviraĠ di base per molte altre considerazioni, per cui mi dilungheroĠ un poco nel suo esame, eĠ la cosiddetta Òbremsstrahlung istantaneaÓ, cioeĠ la radiazione emessa quando una particella in moto uniforme si ferma istantaneamente.
Per quanto questo fenomeno possa sembrare irrealistico, nella realtaĠ eĠ unĠapprossimazione che puoĠ essere usata piuttosto spesso, sia nella sua versione letterale, di un brusco arresto della particella, sia nella sua versione equivalente, dal punto di vista radiativo, di un improvvisa schermatura, e quindi scomparsa, del suo campo elettromagnetico. Questo percheĠ lĠarresto puoĠ essere ritenuto ÒistantaneoÓ per tutte le onde di periodo e lunghezza dĠonda molto maggiori del tempo e dello spazio dellĠarresto vero e proprio.
In generale, se lĠaccelerazione di una particella eĠ limitata nel tempo e nello spazio, la distribuzione angolare ed in frequenza della radiazione emessa, partendo dal campo elettrico dato dalla (1), puoĠ essere scritta, a grande distanza dalla zona dove avviene lĠaccelerazione, come:
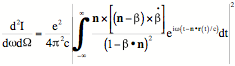(6)
in cui r(t) eĠ il vettore di posizione della particella durante il periodo di accelerazione.
Nel caso di una carica in moto rettilineo uniforme che si arresta istantaneamente, lĠesponenziale diventa una costante.
DĠaltra parte si ha anche che
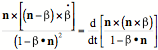
per cui il risultato finale eĠ:
(7)
in cui t0 eĠ lĠistante in cui avviene lĠarresto.
Il termine 
eĠ quindi una fase arbitraria che puoĠ essere del tutto trascurata.
Se b(t0-e)=b0 eĠ la velocitaĠ prima dellĠarresto e b(t0+e)=0 quella dopo, saraĠ
(8)
Nella (8) q eĠ lĠangolo tra la direzione della radiazione e quella di b, si eĠ inoltre mantenuto il segno meno allĠinterno della parentesi per indicare che si tratta di una ÒampiezzaÓ derivante da unĠaccelerazione negativa. Infatti la stessa identica distribuzione di radiazione si avrebbe nel caso di una carica che apparisse improvvisamente dal nulla con una velocitaĠ b0.
Questa situazione eĠ fisicamente rilevabile sia in senso indiretto, quando la schermatura del campo di una particella viene improvvisamente meno, sia in modo diretto nel caso di decadimento beta di una particella o di un nucleo, in cui un elettrone (o positrone) appare improvvisamente, ed eĠ accompagnato esattamente da questo tipo di radiazione elettromagnetica.
In questo caso peroĠ lĠampiezza ha segno positivo, percheĠ deriva da un aumento di velocitaĠ. Se prese indipendentemente, il risultato finale eĠ indifferente al segno, dipendendo dal modulo quadro di questa ampiezza, ma ci sono casi importanti, come vedremo in seguito, in cui entrambe le ampiezze sono presenti contemporaneamente, e quindi devono essere valutate col loro segno.
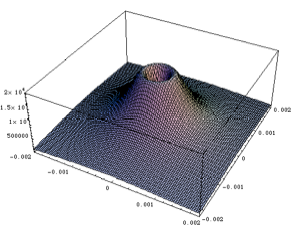
Fig. 4 – Distribuzione angolare della Òbremsstrahlung istantaneaÓ data dalla (8). LĠintensitaĠ eĠ arbitraria, mentre gli assi sono in [mrad]. La figura eĠ calcolata per un g di 2000, corrispondente ad un elettrone da 1 GeV.
La distribuzione angolare data dalla (8) eĠ mostrata in Fig. 4, mentre in Fig. 5 eĠ mostrato lĠandamento lungo una retta passante per lĠorigine.
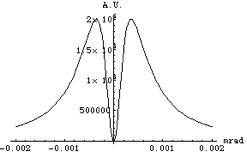
Fig. 5 – Distribuzione angolare data dalla (8) in un piano passante per lĠorigine.
Le caratteristiche principali di questa radiazione sono che, almeno fincheĠ vale lĠapprossimazione con cui eĠ ottenuta, la sua intensitaĠ non dipende dalla frequenza, eĠ una radiazione ÒbiancaÓ. La sua distribuzione angolare ha uno zero nella direzione del moto della particella e un massimo, anchĠesso indipendente dalla frequenza, ad un angolo q=1/g, come puoĠ essere verificato dalla (8) o ancora meglio dalla sua approssimazione per g>>1 e q<<1:
Queste caratteristiche, insieme con altri aspetti, si capiscono meglio se si considera che questa radiazione non eĠ altro che il risultato della libera propagazione del campo dato dalla (5) (o dalla (4) che eĠ equivalente) e dal suo compagno campo magnetico. Come detto nellĠintroduzione, la radiazione elettromagnetica di una particella carica puoĠ sempre essere considerata come generata da una discontinuitaĠ del campo della particella stessa. In questo caso si ha che lĠintero campo della particella dovrebbe scomparire, percheĠ questa si ferma dĠimprovviso. Per mantenere la sua continuitaĠ, nasce un campo radiativo, uguale a quello della particella nel momento dellĠarresto, che si propaga liberamente. NellĠapprossimazione dei fotoni virtuali si ha che questi diventano fotoni reali e si propagano come qualsiasi onda elettromagnetica. Non essendo peroĠ una vera onda piana, la sua propagazione daĠ luogo alla distribuzione angolare data dalla (8). Alcune questioni sottili riguardanti la divergenza del campo originario sullĠasse di simmetria, e la mancanza di tale divergenza nel campo radiativo, verranno analizzate in seguito.
Formalmente, la distribuzione angolare del campo elettrico nellĠapprossimazione di Fraunhofer eĠ data da
(9)
dove E0 eĠ il campo dato dalla (5) e lĠintegrale eĠ esteso su tutto il piano z=0, dove cioeĠ la particella si ferma. LĠintensitaĠ saraĠ poi data da
Il calcolo eĠ piuttosto laborioso, per la presenza della divergenza sullĠasse, ma il risultato finale eĠ esattamente la (8).
Il considerare la radiazione come la libera propagazione dellĠintero campo della particella, intero campo in questo caso di istantaneo arresto, porta a capire abbastanza intuitivamente le proprietaĠ della radiazione stessa.
Ad esempio, lo zero che lĠintensitaĠ della radiazione ha sullĠasse di propagazione eĠ facilmente spiegato dalla natura vettoriale del campo elettrico che, nella (4), ha polarizzazione radiale. Per cui lungo lĠasse z per ogni contributo da un punto di coordinate {x,y} del fronte dĠonda in propagazione, esiste un contributo, identico in ampiezza ma di segno opposto, dal punto di coordinate {-x,-y}.
Anche il fatto che la distribuzione angolare sia
indipendente dalla lunghezza dĠonda e abbia unĠapertura angolare dellĠordine di
1/g eĠ facilmente comprensibile in base
alle semplici leggi dellĠevoluzione ondulatoria. EĠ cosa nota che un fronte
dĠonda concentrato in un raggio piccolo tenderaĠ ad evolvere con unĠapertura
angolare maggiore di uno con raggio maggiore. Nel caso di fasci ottici
gaussiani, come per i laser, lĠangolo di apertura asintotico in caso di
propagazione libera nel vuoto eĠ dato da 
in cui r eĠ
il raggio minimo. Nel nostro caso, in cui non si tratta di fasci gaussiani ma
in cui si ha lo stesso andamento, abbiamo che il raggio di partenza eĠ 
per cui
risulta 
indipendente dalla lunghezza dĠonda, come espresso dalla (8). EĠ cioeĠ
lĠestensione del campo sorgente proporzionale alla lunghezza dĠonda che
determina la distribuzione angolare asintotica indipendente da questa.
Qualcosa di piuĠ si capisce anche se si considera la radiazione che si propaga da un solo semipiano, ad esempio il semipiano y>0. Anche se la cosa puoĠ sembrare un puro artificio matematico, esistono in realtaĠ delle situazioni sperimentali per cui questa eĠ una buona approssimazione, ma le vedremo piuĠ in avanti.
Integrando la (9) in x tra {-°, °} e in y tra {0, °}, si ottiene un comportamento molto diverso delle due polarizzazioni:
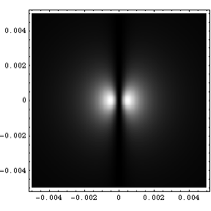
Fig. 6 – Distribuzione angolare della radiazione emessa da un singolo semipiano y>0 in una breemsstrahlung istantanea. A sinistra la componente Ex con polarizzazione parallela al bordo del semipiano, a destra la componente Ey con polarizzazione perpendicolare. Ascisse e ordinate sono in radianti per una particella con 1 GeV di energia.
La componente parallela Ex, poicheĠ il campo cambia ancora di segno per x<0 e x>0, presenta sempre uno zero sullĠasse, mentre la componente verticale, che mantiene lo stesso segno per tutto il semipiano y>0, ha ora il suo valore massimo proprio sullĠasse. EĠ quindi evidente che la distribuzione angolare di Fig. 4 eĠ dovuta alla polarizzazione radiale del campo di una carica puntiforme e dallĠessere lĠevoluzione dellĠintero campo.
A parte una costante di proporzionalitaĠ uguale per entrambe le componenti, le espressioni analitiche delle due distribuzioni angolari da un semipiano sono:
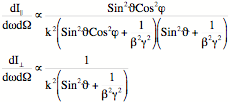(10)
Alcuni dettagli di queste distribuzioni, che possono essere interessanti per unĠanalisi piuĠ avanzata, verranno esaminati a parte.
Gli altri capitoli: